Use second fft or not The second fft is intimately related to the noise blanker. In case you do not need the noise blanker there is usually no need to introduce all the complexity with the second fft, just disable it!If your computer does not support MMX instructions the second fft is not very efficient and you should probably disable it. If your computer supports MMX instructions and if you have access to a pulse generator for calibration, and particularly if your analog hardware has a lot of bandwidth you should definitely enable the second fft if you ever have impulse noise problems. Power line interference, car ignition spikes and alike. The processing that comes after the first frequency conversion is the same regardless of whether the second fft is enabled or not. It is described here: baseband processing in weak signal CW mode
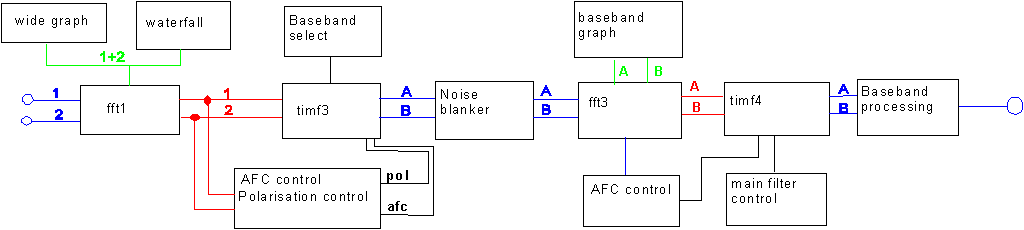
Linrad in weak signal CW mode without second fftFig. 1 shows the block diagram of linrad in two channel mode when second fft is disabled.The first fourier transform, fft1 is the dominating processing task. The output of fft1 is used for several purposes: 1: The averaged power spectrum This is a graph where one can measure signal levels over the full dynamic range of the system. 2: The waterfall graph This is a graph where it is easy to find weak signals. 3: AFC control The history of how the power spectra develop over time is used to select the frequency required to downconvert the selected signal so it will be centered in the narrow baseband filter. 4: Polarisation control The history of how the power spectra develop over time is used to find the optimum combination of the two antenna signals 1 and 2 that will place the signal in output signal A, leaving only noise in output signal B. For an X-yagi receiving a linearly polarised wave the process is equivalent to a mechanical rotation that brings one polarisation in the plane of the incoming wave so the orthogonal set of elements will receive no signal. 5: Decimation filter timf3 is a back transformation of fft1 that uses only a part of the fft1 spectrum. The process is equivalent to a frequency mixing followed by a filter and resampling. Read the data sheet for Analog devices AD6644 or Graychip GC4014 / GC4016 for other ways of doing the same thing (in hardware). Since the fft1 output is already in place for other purposes it is efficient to use it also for the decimation filter. It is possible to handle many different signals in parallel because timf3 operates with a small fraction of fft1 only producing output at a low sampling speed. This way it will be possible to decode many signals simultaneously and print all the transmissions in ascii on the screen.
|
|
The setup screen for parameters related to the first fft is shown in fig.2. The bandwidth and window parameters affect the size of the first fft. The length of the transform is 1/bandwidth if no window is used and it increases with the power of sin used for the window. The minimum processing delay is of course the time it takes to collect all the points needed in the transform so narrow bandwidth in fft1 causes a noticeable processing delay. Table 1 shows some typical values for bandwidth and window parameters and the transform sizes they give at some different sampling speeds.
|

|
The actual bandwidth of each bin in the first fft is not exactly what you asked for with the bandwidth parameter. What you actually get is something approximately within a factor of two. The transform sizes have to be a power of two. It is always nice to have a short processing delay so do not ask for narrower bandwidth than you really can use. A bandwidth of 10Hz is sufficiently narrow to find signals that are so weak that it is impossible to copy them. What window to select depends on the dynamic range requirements and the data decimation ratio.
----------------------------------------------------------------------- | Selected values | real @ 6000Hz|real @ 44100Hz|complex @ 44100Hz| | | | | | |Bandwidth Window |Size Bw Delay|Size Bw Delay| Size Bw Delay | |parameter parameter | | | | ----------------------------------------------------------------------- | 200 3 | 128 56 0.04| 512 103 0.02| 1024 103 0.02 | | 20 2 | 512 12 0.17| 4096 11 0.18| 8192 11 0.18 | | 5 1 | 1024 4 0.34| 8192 4 0.37|16384 4 0.37 | | 1 1 | 8192 0.6 1.36|16384 2 0.74|65536 1 1.48 | ----------------------------------------------------------------------- Table 1. Typical fft sizes, bandwidths and processing delays for different combinations of fft1 parameters. The bandwidth is calculated as 1/t where t is the time between the 6 dB points of the window function. When narrow bandwidths are used (large fft1 size) a low order window is sufficient but if the first fft bandwidth is large the window should be of higher order. The data decimation means picking a part of the spectrum, then transforming that part only backwards. Spurs are produced if there is a signal that has part of its energy within the selected point and parts outside. The spurs will mainly fall at very low and very high frequencies in the back transform so they will to a large extent be filtered out in the next filtering process. Some of the spur energy will fall at the frequency where the desired signal is and those spurs may limit the dynamic range if unsuitable parameters are selected. The whole thing is quite simple. Select the parameters that make a strong signal as narrow as you want it in order to find weak signals close to it on the main spectrum. The limit is not often linrad, it is the sidebands of strong interfering signals that limit how close you can go before interference is a problem. To get an idea, check the screen dumps showing the resampling spurs from fft1 back transformation with some different parameter choices. These graphs clearly show that resampling spurs is not a limiting factor for system performance. When you have decided what bandwidth and window to use, try the different fft versions and select the one that works fastest on your computer. The parameter First FFT max avg time is used to determine how much memory to reserve for first FFT spectra. This parameter also determines the maximum time the AFC and adaptive polarisation may base the signal tracking on. First FFT amplitude is a scale factor, 10 times here is 20dB. This scale factor will shift the signal level everywhere within linrad. When second fft is disabled, moving the y scale does not affect processing since floating point arithmetics is used everywhere.
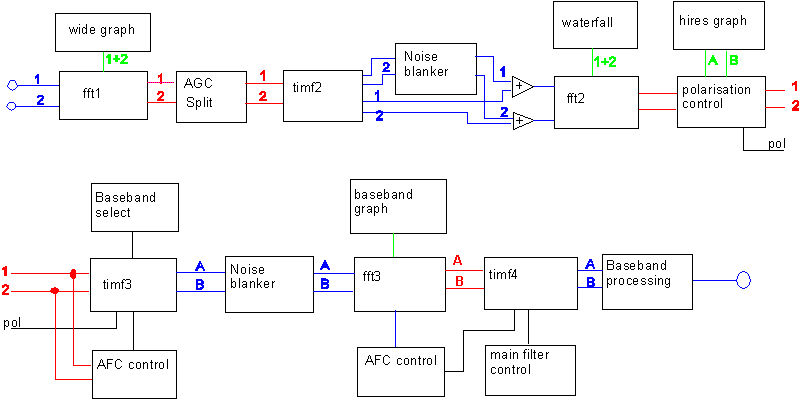
Linrad in weak signal CW mode with second fft enabled.When the second fft is enabled the first fft is used primarily to split the incoming signal into a weak signals part and a strong signals part.The first fft produces a full dynamic range power spectrum on the screen and points which are considered strong come in red colour. Red and white points are grouped together in two transforms. The one with strong signals is reduced in amplitude to fit in 16 bit words while weak signals automatically fit in 16 bits. Weak and strong signals are back transformed separately to provide two time functions, one of which contains only noise and weak signals on which the noise blanker operates. The second fft then makes fourier transforms of the sum of the weak and the strong signals. Figure 3 illustrates linrad running with two rx channels and with second fft enabled. When the second fft is enabled it is essential to set gain levels correctly all the way through linrad. timf2 and fft2 use 16 bit only to take advantage of the very fast 16bit MMX instructions.
|
|
Setting up the first fft When the second fft is enabled, the purpose of the first fft is only to remove strong narrowband signals that would destroy the noise blanker performance if they were left in place. There is no reason to waste computer time doing the first fft too well unless there are very strong signals of very high quality within the passband. Some screen dumps are presented to illustrate this. Typical bandwidth to use for the first fft is 100Hz with a sin to power 3 window. In case the second fft is made very large somewhat narrower bandwidth for the first fft may be useful because the ratio between the transform sizes affects the signal level at which a signal is regarded as strong. With a very large ratio between transform sizes some of the desired signals will be strong enough to be routed together with the strong signals and then they will suffer from poor noise blanker performance. When the second fft is enabled the first FFT amplitude parameter that changes the signal level has to be adjusted together with other parameters to place the signal correctly in the 16 bit format of timf2 and fft2. For details, look at set digital signal levels correctly The second fft is used for: 1: The waterfall graph This is a graph where it is easy to find weak signals. 2: The high resolution graph This graph is complementary to the waterfall graph. It is an averaged power spectrum and with long averaging times it becomes extremely sensitive. This graph presents the spectrum with one pixel per point while the waterfall only has 1024 points and often has a large number of data points behind each pixel which causes loss of S/N. 3: AFC control The history of how the power spectra develop over time is used to select the frequency required to downconvert the selected signal so it will be cerntered in the narrow baseband filter. 4: Polarisation control The history of how the power spectra develop over time is used to find the optimum combination of the two antenna signals 1 and 2 that will place the signal in output signal A, leaving only noise in output signal B. For an X-yagi receiving a linearly polarised wave the process is equivalent to a mechanical rotation that brings one polarisation in the plane of the incoming wave so the orthogonal set of elements will receive no signal. 5: Decimation filter timf3 is a back transformation of fft2 that uses only a part of the fft2 spectrum. The process is equivalent to a frequency mixing followed by a filter and resampling. Read the data sheet for Analog devices AD6644 or Graychip GC4014 / GC4016 for other ways of doing the same thing (in hardware).
|

|
The second fft is never smaller than the first fft. How much bigger it is is set with the bandwidth factor, see fig. 4. The same rules apply for spur generation when fft2 is back transformed as when fft1 is back transformed. To get an idea, check the screen dumps showing the resampling spurs from fft1 back transformation with some different parameter choices. These graphs clearly show that resampling spurs is not a limiting factor for system performance. For the second fft, select a window 0 to 2 depending on second fft size. The second fft does not have any strong signals ever so spurs is less of a problem. The first backward FFT version is very important. If your computer has MMX, select 1 here. It has a significant effect on processor load. The second forward FFT version is equally important. If you have MMX, select 2 here. The att N parameters control how the signal levels grow while the transforms are computed. These parameters have to be set properly to not saturate the 16 bits or to lose S/N ratio due to quantisation noise. For details, look at set digital signal levels correctly The parameter Second FFT average time is used to determine how much memory to reserve for second FFT spectra. This parameter also determines the maximum time the AFC and adaptive polarisation may base the signal tracking on.
|