|
Note that the information on this page is only applicable when
16 bit MMX instructions are selected for the first backward FFT
and/or the second FFT. If your computer has CPU power for the 3 times slower
float algorithms, use float and do not worry about the information on this page.
Skip many words and go to the practical procedure of setting up linrad correctly Maximum number of bits in the input signalAt the present time (year 2001) the standard audio board samples 16 bit at 44.1 or 48kHz. There are boards that are sold as 24 bit 96kHz but as often in the HIFI industry, hardware is overspecified. When actually sampling at 96kHz the number of bits is much lower than 24. The 24 bit board will give perhaps 10dB more dynamic range, not 48 dB as one would expect from 8 more bits.The maximum S/N for an A/D converter is 20 * log(N) + 10 * log(12) which evaluates to 107.1dB for a 16 bit A/D converter with N=65536. When sampling at 44.1kHz, the bandwidth is 22.05kHz so the noise floor due to quantisation noise is at -150dBc/Hz. (dB below a near saturating carrier in 1Hz bandwidth) This formula implies that the noise floor due to quantisation noise is 0.29 bit RMS In real life quantisation noise is eliminated by allowing some extra smaller bits that sample essentially amplifier and thermal noise. As a consequence the noise floor is normally something like 20dB above the quantisation noise limit. This means that the degradation when loosing one or a few bits is very small - the smallest bits contain mainly noise. This is no critisism at all. To make the quantisation noise contribute to the total noise by 1% only, the noise floor has to be placed 20dB above the quantisation noise. Experimentally, a 16 bit soundblaster PCI gives a S/N of about 115dB at 25Hz bandwidth or 139dBc/Hz as measured by linrad. This is 11dB above the quantisation noise limit. If two bits are cleared before the signal is further processed, performance is degraded by 4dB, the noise floor is at 135dBc/Hz while the quantisation noise limit is at 138dBc/Hz. Removing 3 bits from the degrades the measured value to 130dBc/Hz. When 3 bits are removed, practically only quantisation noise is determining the noise floor. The discrepancy with the theoretical value, 2dB is because the bandwidth in linrad is not quite the noise bandwidth, it is a bandwidth calculated from 1/time for the 6dB points of the fft window function. Dynamic range values measured by linrad are always underestimated by 2dB throughout this site SM5BSZ / Linrad Home Page A modified Delta44 soundboard gives a dynamic range of 146dBc/Hz when sampling at 96kHz. When talking about number of bits it may be reasonable to compare to a A/D converter having the quantisation noise at 168dBc/Hz, 20dB below the actual noise floor, taking the 2dB bandwidth error of linrad into account. Sampling at 96kHz means a bandwidth of 48kHz so the maximum S/N in full bandwidth is 121dB. According to the formula above we have:
16 bit 107.1dB
The modified Delta44 can be characterised as a 18 bit A/D converter with the noise floor 18dB above the quantisation noise. In its original shape the Delta44 can be characterised as a 18 bit unit with the noise floor 21dB above the quantisation noise. When the Delta44 is run in 16 bit mode, the quantisation noise is increased by 12dB. The other contributions to the noise floor are 6 dB higher for the modified board so running the Delta44 in 16 bit mode leads to a loss of 1 dB only. In its original shape the loss from running the Delta44 as a 16 bit converter is only 0.5dB! Based on the performance of currently available A/D converters it seems reasonable to design linrad for 19 bits of valid input data.
Dynamic range of the output from the first fftWhen running linrad at wide bandwidths the first fft is used only to separate out very strong signals so the noise blanker can operate properly. For this purpose there is no reason an fft with much narrower bandwidth than the strong signal. This means that the size of the first fft is typically 4096 (N=12) when linrad is run at maximum bandwidth.Assuming that 19 data bits of the input is more or less valid a near saturating signal will need 31 bits after the 12 butterfly loops that each multiplies the level by two. The noise floor from the A/D converter which is represented by 2 bits will grow by the square root of two for each loop since the two voltages added are uncorrellated. The noise floor is therefore represented by a number corresponding to 8 bits. The first fft of linrad is performed with floating point numbers. They use 23 bit for the mantissa so worst case rounding errors are 8 bits. This is an error in the strongest signal and it is completely insignificant. The rounding errors of the previous fft loop will go into the noise floor at some frequency where there should be no contribution at all from the strong signal. Two large numbers, both with 7 bit rounding errors are combined and they produce a noise contribution at one frequency that is 3dB below the A/D noise floor. The 4 byte floating point arithmetics is enough to preserve the dynamic range of a 19 bit A/D converter with a noise floor that is 12dB below the noise of a modified Delta44. The strongest signal may be 23 bits above the noise floor and the noise floor has to be represented by 2 to 3 bits to avoid introduction of quantisation noise so the fft1 output needs 26 bits when represented as integer numbers. In order to allow the fft1 back transformation with MMX instructions it is necessary to separate out all frequencies that need more than 16 bits. The time function that results from the fft1 back transformation will be used as input to the second fft which may be several times larger. If fft2 is selected to be 65536 (N=16) it is necessary to limit the strongest frequency in the fft1 output to 12 bits only since an owerflow could otherwise occur in the second fft. The zero point of the main fft displaySince the first fft is calculated with floating point numbers it does not matter where the zero point is placed for the transform itself or its display. If the second fft is disabled you can shift the spectrum up and down the dB scale by use of the parameter First FFT amplitude which is 2000 by default. You will have to adjust the output audio volume accordingly but processing is not affected.When the second fft is enabled, the output of the first fft is rounded to integer values and it is essential that the white noise floor is placed high enough above the quantisation noise caused by loosing the floating point decimals. For the noise blanker to operate it is essential that the noise floor is placed low enough. More about that below. 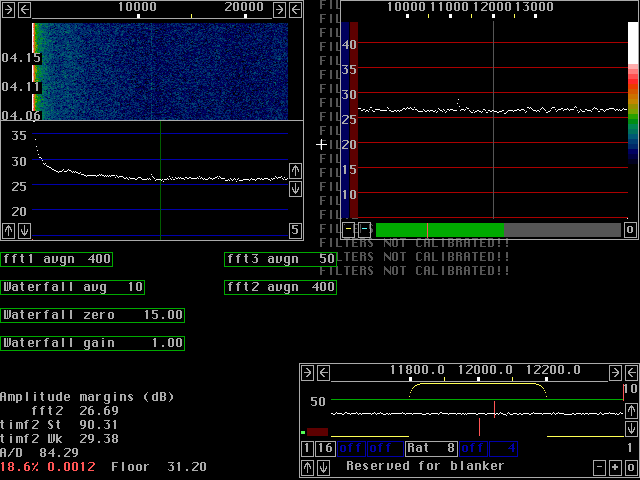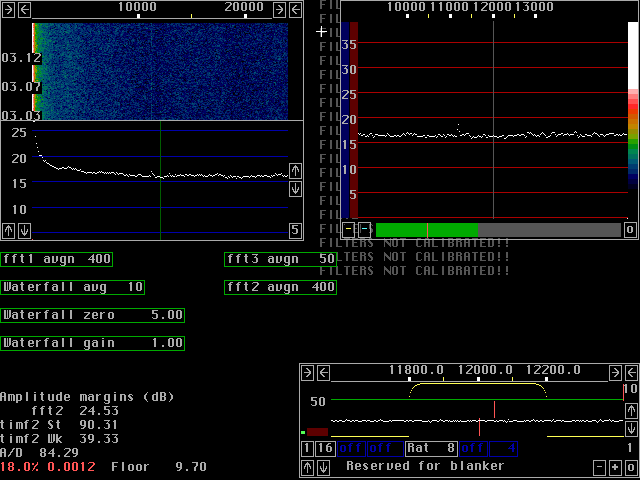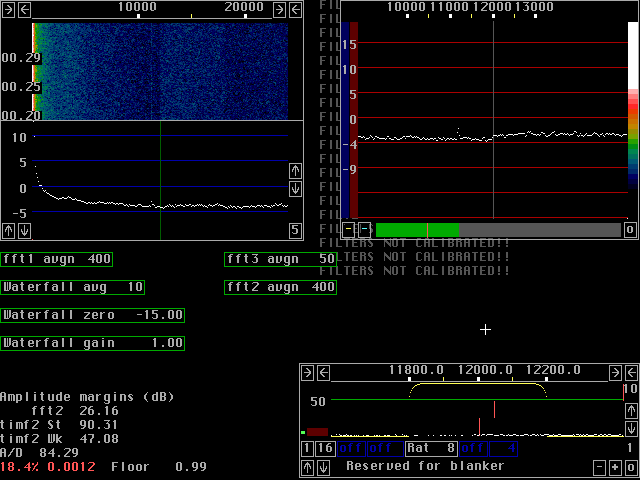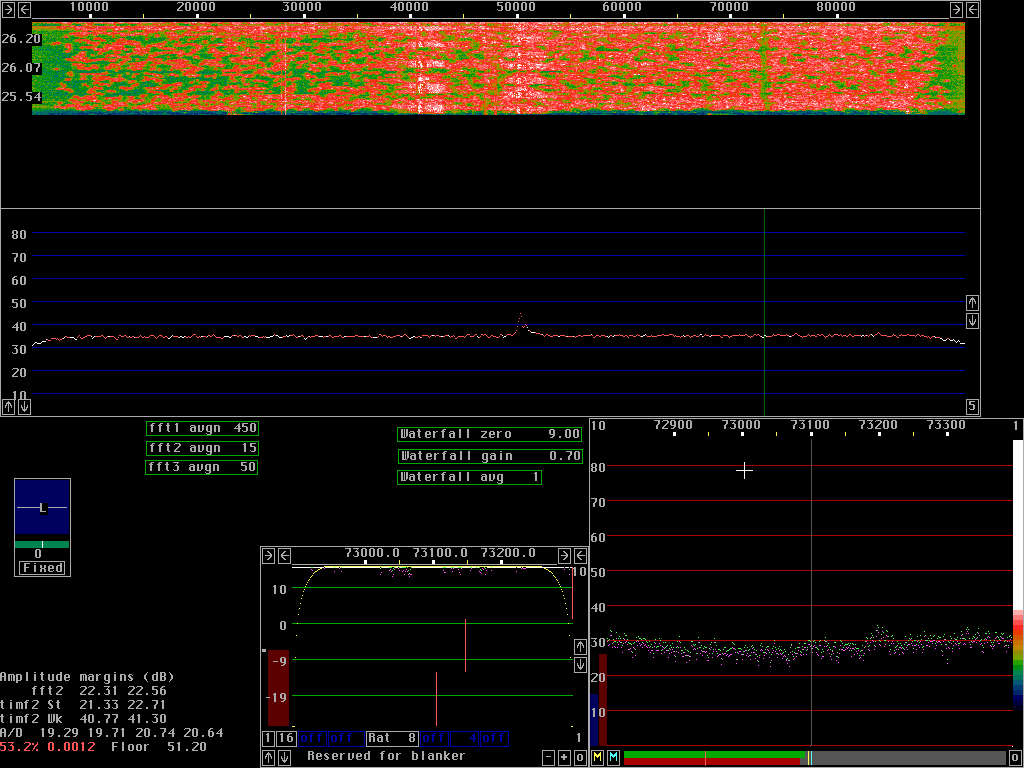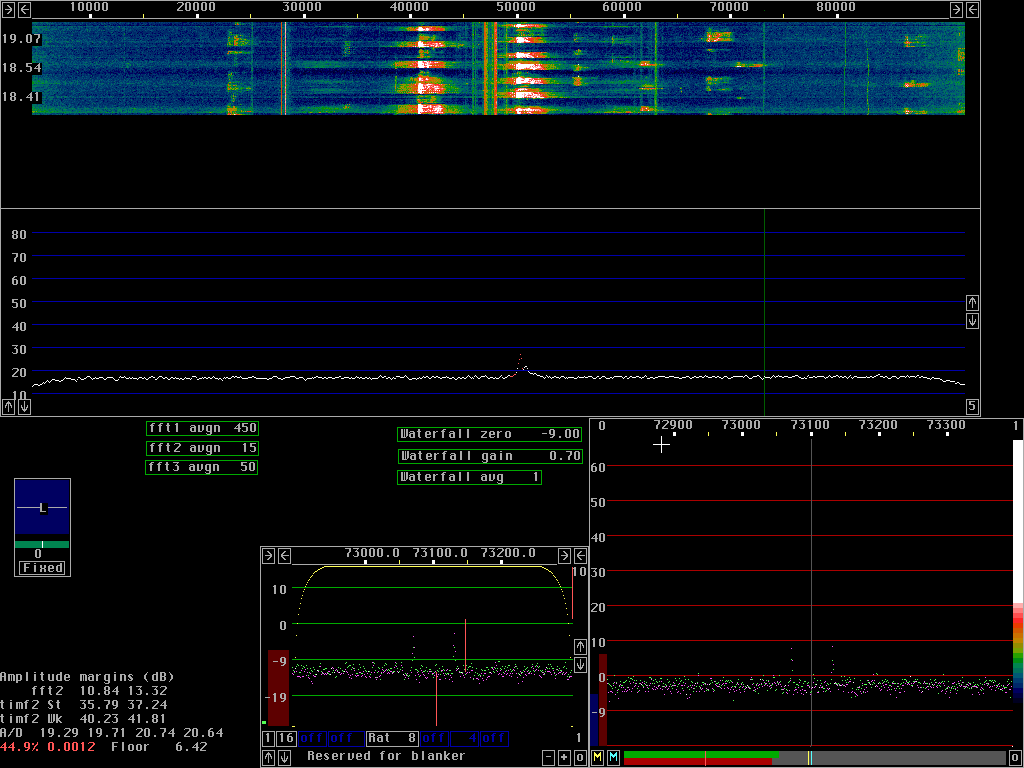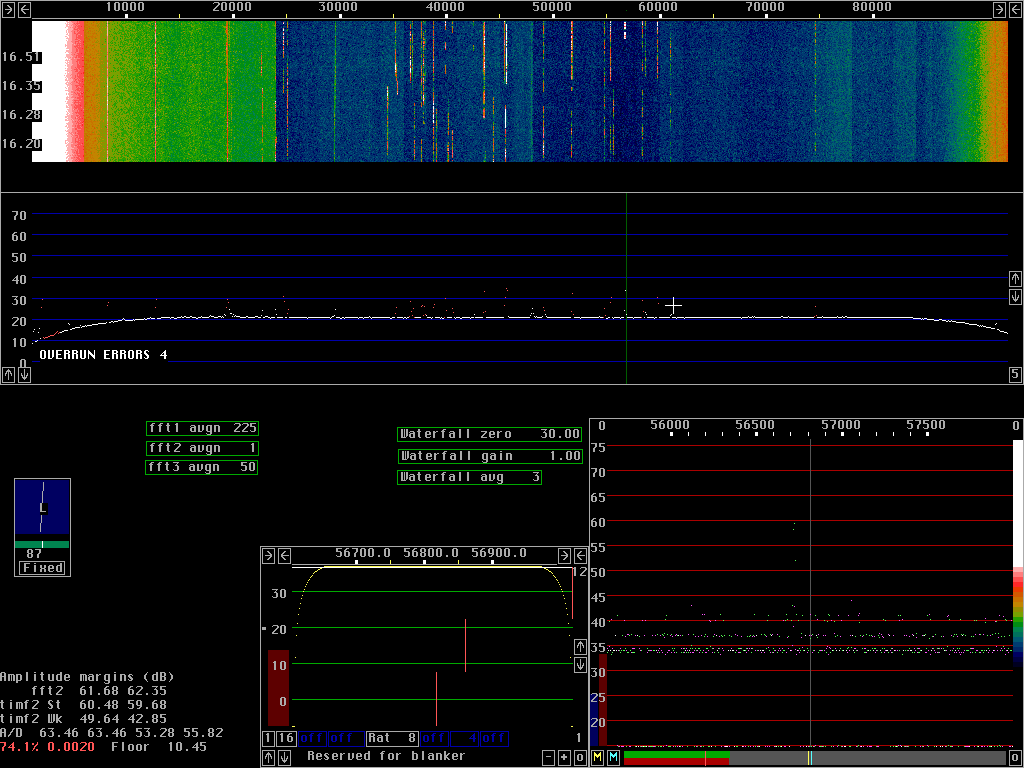Compare the figures 1 to 5. These figures are produced from exactly the same input from the A/D converter (stored on the hard disk). A weak tone at 11.2kHz is injected into a Delta44 sampling at 96kHz. The size is 2048 for both fft1 and fft2 with sine to power 4 windows for both. The x-axis is one pixel per bin for both fft1 and fft2. Note that the second fft gain parameters have to be adjusted to keep the processing within 16 bit to avoid introduction of other rounding errors (more about them further down this page). 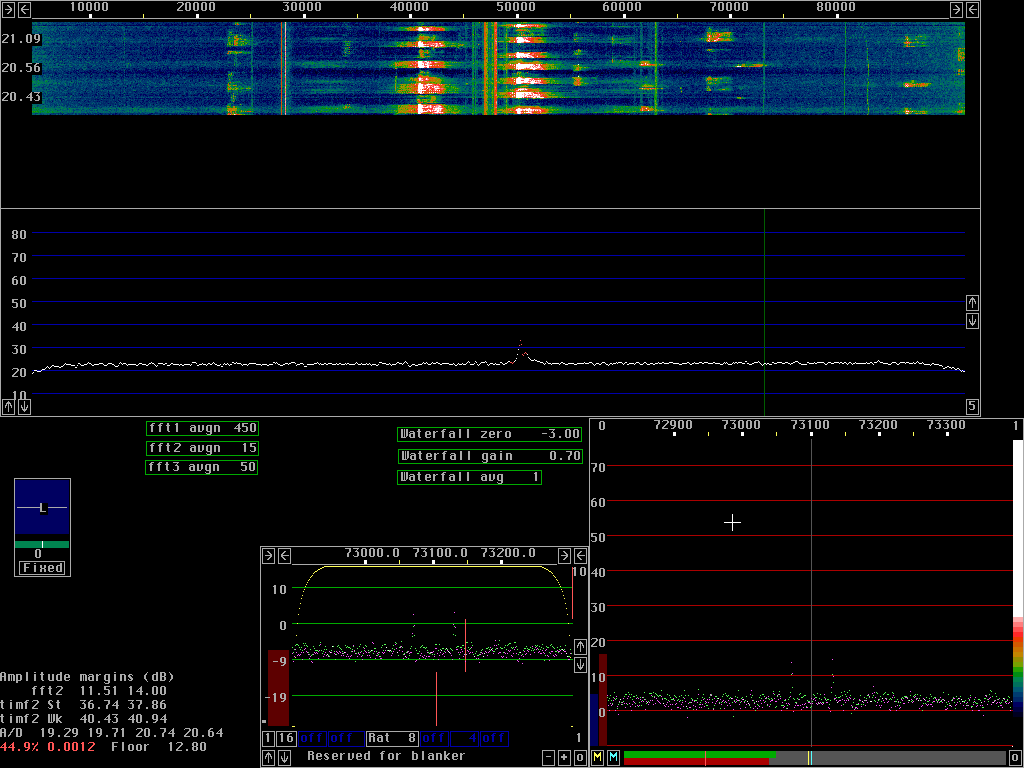To set First FFT amplitude, first press A to get the amplitude information in the lower left corner. The bottom line gives the noise floor in bits RMS. If you have a nice location with a noise floor that is essentially white noise of constant amplitude, you should find the noise floor somewhere between 10 and 30 dB when using the default parameter value 2000. The Floor RMS value should be in the range 3 to 30. The soundboard itself should be somewhere between -5 and +5dB and your analog hardware should add between 15 and 25 dB. In most situations there is no reason to do anything, just use the default value of 2000. In case your hardware is not properly adjusted you should change the First FFT amplitude parameter to place your white noise background somewhere in the 10 to 30 dB range..
|
|
The most critical situation is if you want to run a small first fft
and a very large second fft in a location with extremely bad
powerline noise.
To show what the problem is, the data used to demonstrate the noise blankers was used with extreme fft size parameters. The first fft size is set to 1024 and the second fft is set 65536. Such large size ratios should not be used normally, there is no reason. The large size ratio makes linrad reserve 6 bit for signal growth in the second fft, one bit for sign and one bit for the noise floor being calculated as the average of I and Q for two rx channels. There is also one bit of safety margin so in this case only 7 bits are allowed for weak signals and noise. The test signal has powerline noise that reaches 25dB above the white noise floor. Since 25dB is nearly 6 bits there is only one bit left for the white noise floor which then comes very close to the quantisation noise at about 0.3 in units of one bit. When the noise floor (powerline noise) is placed at 35 dB on the main fft display it is already too strong to be considered by linrad to be noise or a weak signal see fig. 6. Far too many frequencies are considered as strong signals, they are coloured red and the noise blanker does not work. Note that the fft1 gain parameter is 20dB smaller than normal because I added 20dB of extra RF gain to overcome hum at the center of the passband. Since no strong signals are present this loss of 20dB of the dynamic range is completely without any adverse effect. The remaining figures on this page show the screen with the "First FFT amplitude" parameter stepped downwards in 6dB steps. Other parameters are adjusted to keep the signal levels constant further down the signal path. Only the rounding errors at the first fft output affects the S/N in figures 6 to 10. |
Fig 8.
First FFT amplitude = 20.
The white noise floor is at about -3dB in the fft1 spectrum,
25 dB below the powerline noise and 8dB above the quantisation noise.
There should be a very small loss of S/N but I can not see it.
Everything still works fine.
Fig 9.
First FFT amplitude = 10.
The white noise floor is at about -9dB in the fft1 spectrum,
25 dB below the powerline noise and 4dB below the quantisation noise.
Subtle differences can be seen in the noise floor of the
high resolution graph.
Fig 10.
First FFT amplitude = 5.
The white noise floor is at about -15dB in the fft1 spectrum,
25 dB below the powerline noise and 10dB below the quantisation noise.
Surprisingly enough, the weak signals in the high resolution graph
have lost only 2dB of their S/N.
The fft1 back transform gainThe output of the first fft is limited to fit with a good margin in 16 bit. That is in the frequency domain. When the back transform is taken, any pulses present may reach large amplitudes. Saturation should be avoided. Press A to see the amplitude margin information. Use the parameter First backward FFT att N to set the timf2 St and Timf2 Wk margins. This parameter determines how many loops in the back transform that are run with a shift instruction that divides by two to stop further growth of the time domain signal. If the parameter is too large the margin will become very large and not enough bits will be used for the timf2 signals.The noise floor that remains with the weak signals is displayed as horisontal bars in the high resolution graph. The red vertical line is at 20dB over a single bit. There is no reason to place the noise floor higher than that although it makes no harm as long as there is a margin shown in the table you get by pressing A.
The second fft gainThe second fft gain is controlled in the same way as the first backwards fft. Set the parameter "Second forward FFT att. N" to get a reasonable margin for fft2, the first line in the data obtained by pressing A on the normal screen.Fig.11 shows what happens if the attenuation is far too low. The fft2 margin is 62 dB. The high resolution graph shows that the power at many frequencies is zero so all information on those frequencies is lost. Loosing bits is a rounding error and it goes different ways above and below 25% of the Nyqvist frequency. If the noise floor is at 1.5bit, rounding up or down will make a difference of 6dB!!! The maximum amplitude that can occur in the second fft is limited by the selective limiter. There is never any reason to have a big margin here. 30dB is normally enough to get the noise floor with many enough bits but there is nothing wrong with a smaller margin as long as it is above zero.
|
