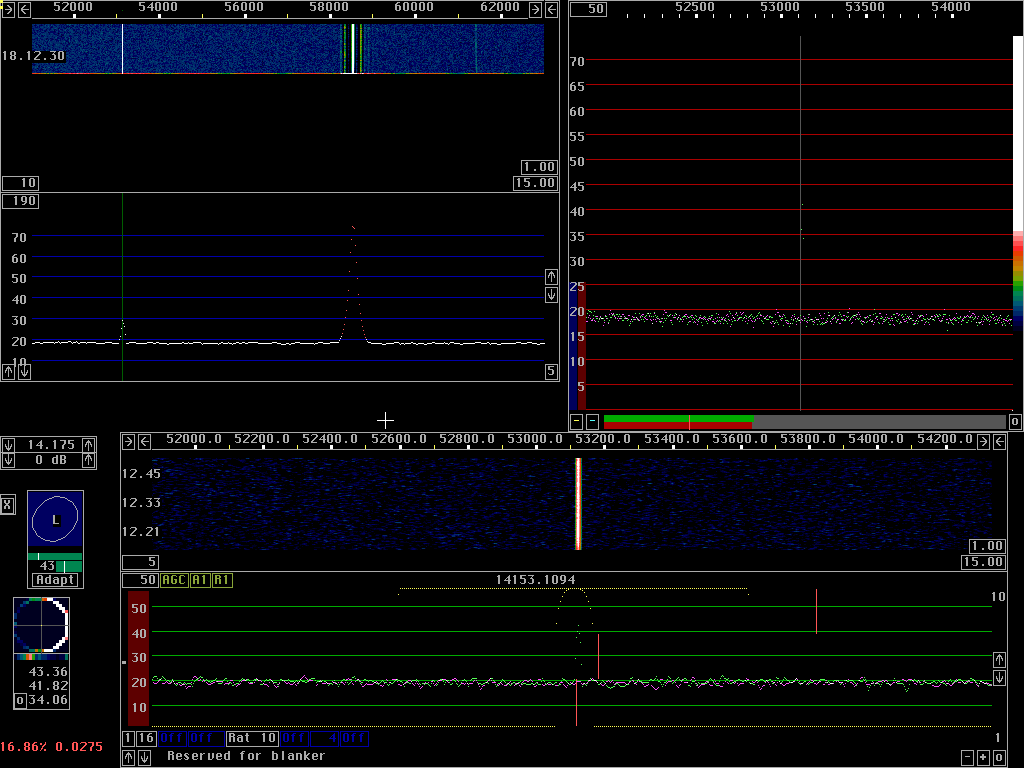
The noise blankerA conventional noise blanker operates in a bandwidth of something like 15 kHz. It detects whenever the voltage of the signal within the passband is above normal and sets the signal to zero during such time intervals. The problem with a conventional blanker is that it zero is not the correct voltage to set during the interference pulse in case there is one or more strong signals within the passband. Setting the voltage corresponding to strong signals to zero is the same as keying the strong signals, something that is associated with keying clicks. By use of a narrower bandwidth one can reduce the risk of getting unwanted strong signals into the passband, but blanker performance is then degraded by the lengthening of the pulse and the correspondingly longer times during which the desired signal is lost.One way of solving the problem when a noise blanker is implemented in a digital radio is to not set the signal to zero during the duration of a pulse, but to some value found by an interpolation from surrounding data points in the signal. Linrad uses this strategy in its most extreme form. The input signal is split into two parts. One, called strong signals that contains all those frequencies outside the desired passband on which the averaged power spectrum shows that narrowband signals are present, another, called weak signals that contains all other frequencies including the desired frequency band. The blanker operates on the weak signals which by definition does not contain any strong signal besides possibly the desired signal. When the two parts are subsequently summed, the final waveform is not zero during the duration of the pulse, it is a perfect interpolation over the time of the pulse using a fit in the FFT size to all the signals present among the strong signals. The conventional blanker the dumb blanker in linrad operates as described above. In case the desired signal is a strong signal, the dumb blanker does not remove any pulses, it just replaces the pulses with keying clicks caused by keying the strong signal. That does not matter much because such keying clicks are in general much weaker than the desired signal itself. The conventional blanker will of course not remove the parts of the noise pulses that fall within the frequencies of the strong signals. Besides the conventional blanker, Linrad has a pulse fitting and subtraction algorithm, the smart blanker which subtracts the most probable waveform associated with the interference pulse assuming that the pulse is wideband and therefore has a shape that is given by the pulse response of the hardware. The smart blanker does not produce any keying clicks, it is a linear process and it does not modulate any signal. Since the correct shape of the pulse is subtracted from the weak signal, the subtracted pulse will have energy within the frequency regions contained in the strong signals and this will cancel the pulse equally well at these frequencies provided that the gain is the same for the weak signals as for the strong signals. When using 16 bit arithmetics this is not possible, the strong signals are then subjected to a selective AGC that turns down the signal level for everything to fit within 16 bits. This has been necessary because the 16 bit MMX instructions are about three times faster than floating point or 32 bit integer arithmetics. In recent years, with the Pentium IV, it has become possible to use 32 bit floating point instructions without CPU overload and this makes Linrad easier to use because setup becomes much less critical. Setting the digital signal levels correctly is critical to preserve the good dynamic range of 24 bit A/D converters. With floating point arithmetics this problem disappears. Screen dumps showing blanker operationThe images below show the Linrad screen on 14 MHz. The main spectrum is zoomed in to cover 12 kHz from 14.151 to 14.163 MHz. The WSE converters are used and the gain is set to 0 dB. The signal at 14.1531 MHz is -123 dBm, while the signal at 14.585 is at -77 dBm. Both signals are carriers from signal generators. All images have these two signals, some also have noise pulses with an amplitude of 0.5 V and a repetition rate of 73 Hz. The pulses have an essentially flat power spectrum from DC to 20 MHz. When filtered through the 93 kHz passband of the WSE converters, the pulses have a peak amplitude of -54 dBm, 23 dB above the signal at 14.163 MHz. In SSB bandwidth the peak power of the pulses is about 10 dB below the power of the signal at 14.163. All signals are fed to both inputs of the RXHFA unit through a hybrid and the power levels given are the power levels at each input. |